
| |
 |
|
|
James T. Townsend Lab
Department of Psychology
Our research aims to integrate three conceptual levels of research (theoretical, methodological and empirical) in order to develop veridical mathematical models of cognitive processes. The following table presents an overview of the manner in which three levels of psychological experience intersect with the three conceptual levels of analysis (theoretical, methodological, and empirical) that we hold to be requisite for a complete account of cognition. 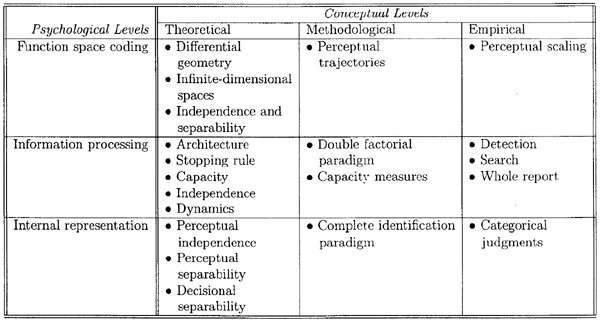 First Psychological Level of Analysis: Function Space Coding We here encounter the first, and perhaps one of the most challenging, theoretical issues: We need to be able to provide an account, at a suitable level of abstraction, of the perceptual code for this instant in visual time (as discussed in O'Toole, Wenger & Townsend, 2001). Central to the development of such a code are theoretical languages capable of characterizing the numerous shifts in energies across the visual field. One promising basis for such language can be found in the mathematical discipline of differential geometry. Differential geometry combines classical notions of space, angle, distance, and so on, with the powerful apparatus of the calculus. It is safe to say it has revolutionized the study of surfaces and much more complex spatial objects, some of which cannot even be pictured in our ordinary kinds of spaces (at least in such spaces of comparable dimensionality). One important branch is that of Riemannian (in honor of Riemann, one of the inventors of non-Euclidean geometry) manifolds (one particular type of space). A Riemannian manifold looks locally like an ordinary Euclidean space, but can require a way of measuring distance and size that differs greatly from the Euclidean. The earth is a good intuitive example of a Riemannian manifold: locally, we can treat it as flat (i.e., Euclidean), but if we measure the shortest distance between two points we get a great circle, not a Euclidean straight line. Riemannian geometry provided Einstein with the essentials he required for his general theory of relativity and we believe it offers a promising milieu for investigation of potentially quite complex psychological spaces. A critical accomplishment of the prior period of support was the development of a nascent and rich theoretical language, based on differential geometry, for describing initial 3-D object (e.g., faces) information. Second Psychological Level of Analysis: Information Processing Hypotheses for the processing of this information need to explicitly consider four basic issues about the characteristics of processing (e.g., Townsend & Ashby, 1983; Townsend & Nozawa, 1995): 1. How are the processes handling these sources of input information arranged in space and time (i.e., what is the process architecture)? Theoretical alternatives include serial, parallel, and coactive arrangements. We hypothesize that interactive parallel or coactive processing architectures support configural percepts. 2. What algorithm or rule does the processing system use to determine when a response can be generated (i.e., what is the stopping rule)? Alternatives here include self-terminating (or minimum time) and exhaustive stopping rules. We contend that a strong representation of configural processing demands an exhaustive stopping rule, against perhaps, traditional assumptions regarding inefficiency of exhaustive processing. However, if the object is virtually processed as a single "point-like" thing, the processing could be extremely efficient (e.g., super capacity) though complete (i.e., exhaustive). 3. What is the relationship among the rates of processing in each of the processing channels of any prescribed set of feature channels? Strikingly almost all processing models of object processing have assumed independence (but, cf. Rumelhart & McClelland, 1982; Mordkoff & Yantis, 1991; Townsend, Hu & Evans, 1984). Even in non-configural settings, that assumption may be incorrect (e.g., Busey & Townsend, 2001), and we hypothesize that any designated parts of a configural object will evidence strong positive dependencies. An issue that is often confused with independence is separability. Separability is defined as an average invariance of a percept of a dimension or feature across experimental variation of another dimension or feature in the same object or set of objects. Separability refers to an across-stimulus property whereas independence refers to a within-stimulus property. Nevertheless, both separability and independence are associated with non-gestalt, non-configural kinds of stimuli and consequent percepts. 4. How does the performance of the perceptual or cognitive system change as the demands on the number of elements to process is varied (i.e., what is the system's capacity)? We hypothesize that the overall object can be processed with less capacity expenditure than can any subsets of it, a super capacity edict. Some of our recent work has shown that dependencies among channels responsible for processing respective dimensions or features can significantly impact capacity. Super capacity and positive channel dependencies are both, in our view, good candidates for gestalt perception and can readily appear together in dynamic processing systems (Townsend & Wenger, 2002). Such a system will not only be non-independent but will also typically exhibit non-separability. Third Psychological Level of Analysis: Internal Representation At the third level of analysis, we can pose questions about cognitive processing in terms of the nature of the psychological representation of the stimulus. Here we are not so much concerned with the nature of the processes that operate on the internal codes as we are with the multidimensional nature of the codes themselves (see discussions of the distinction in Massaro, 1998; O'Toole et al., 2001; Thomas, 1996; Wenger, 1999). Returning to our example of an observer making an affect judgment, imagine that the observer must use the information about both the eyes and mouth to make a judgment that reflects the unique combination of the various states of each of the features (e.g., responding to a smile in the mouth without any discernible happiness in the eyes as being disingenuous). This is a situation that corresponds to a prototypical experimental design known as a complete identification task, and is one that has been of critical importance for a developing the multidimensional generalization of signal detection theory known as general recognition theory (GRT, Ashby & Townsend, 1986; Thomas, 1995, 1996; Townsend, Hu & Evans, 1984). GRT provides rigorous, consistent definitions for a set of constructs pertaining to aspects of representation that, prior to GRT, had been subsumed under terms associated with the notion of configurality, such as integrality (e.g., Garner, 1974j Maddox, 1992). GRT makes distinctions between perceptual and decisional sources of configurality, and between configurality that can exist within the information for a single stimulus and configurality that exists in the effects due to variations across stimuli. For example, configurality at the level of a single stimulus could be due to a violation of perceptual independence (PI, as it is rigorously defined in GRT). In this type of configurality failure, two parts of a figure (e.g., features or dimensions) would interact, in the sense that the accuracy on one depends probabilistically on the accuracy on the other-within a specified stimulus. Configurality failure could also be due to the presence of perceptual separability (PS) (in Garner's (1974) terms, non-integrality), something that would be evident across variations in stimuli rather than within a single stimulus. Thus, as mentioned earlier, the setting on one dimension (e.g., a smiling vs. neutral mouth) would affect the general perception of another dimension (e.g., the perceived average length of a red rectangle). Finally, a "weak" form of configurality could be obtained by systematic shifts in an observer's decisional criteria across variations in stimuli, referred to as a violation of decisional separability (DS). | ||||||||
|
Contact the Webmaster.
Last updated:
27 February 2024
|